oneDNN Adventures
Tilmann E. Bartsch, 04.03.2023
CPU Integer matrix-matrix multiplication using numpy is catastrophically slow. Other solutions
are only slightly better. For x86_64 CPUs, Intel's C++ library oneDNN provides a remedy. See
numpy-int-ops
for a working implementation.
The neglected son: Integer Matrix Multiplication
Large matrix-matrix multiplications of two int8-matrix accumulated in an int32 matrix in numpy are painfully slow.
The computation time is actually more than 10x slower than for float32 values, although the latter require four times more memory space per value!
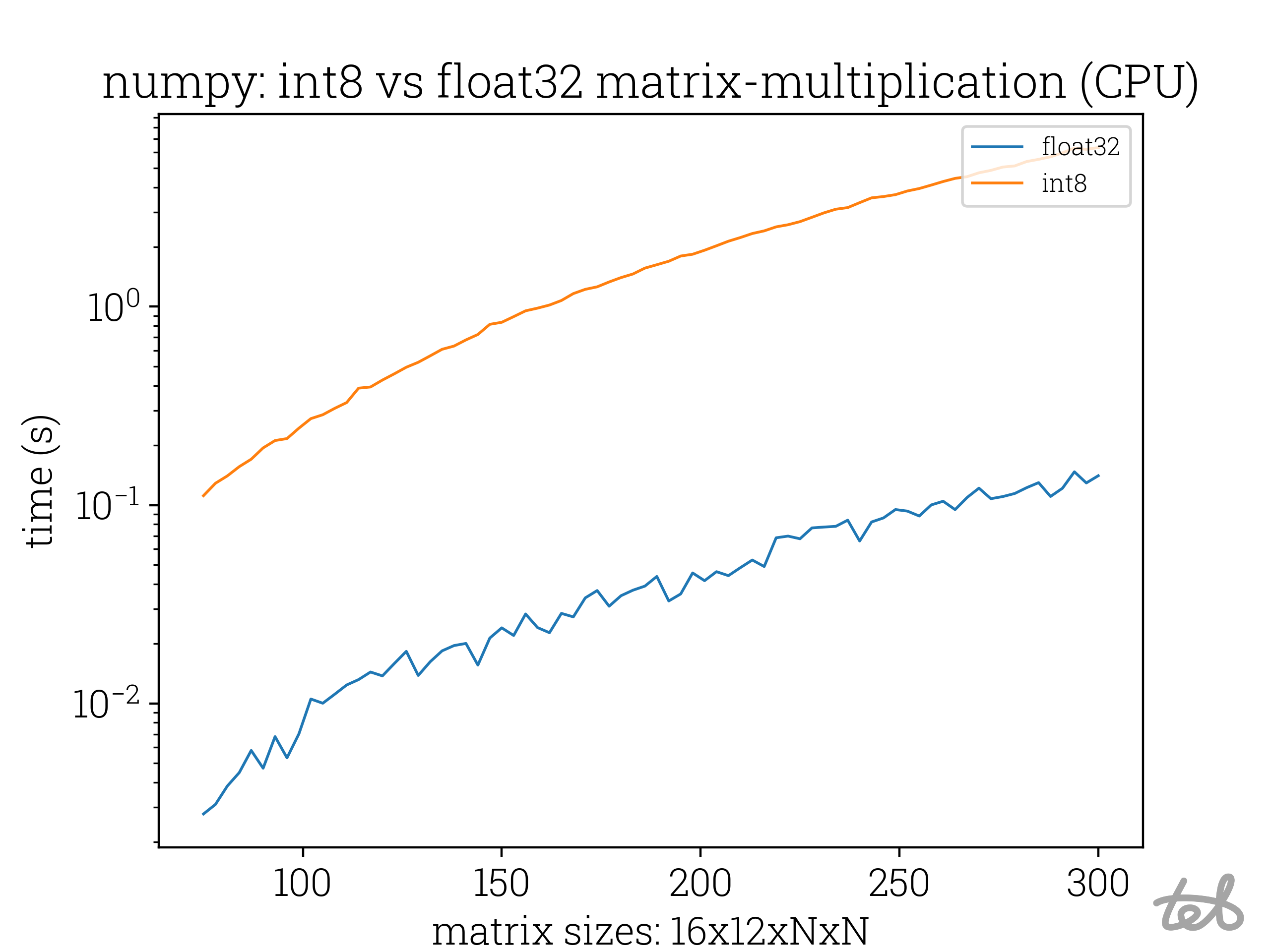Runtime Analysis of the matrix-matrix multiplication of two identical matrices for differing values of N. In the case of
int8-integers the accumulation is performed with int32-integers.
What the fuck! Just wanted to make some simple operations and now everything turns out to be an order of magnitude slower? Turns out that numpy is based on BLAS (Basic Linear Algebra Subprograms) which is heavily optimized for floating point computations but not at all for integer calcuclations.
I assume that until the dawn of quantization methods for neural networks, nobody cared about this specific integer operation. If that's correct, the next best thing to go are neural network libraries supporting some kind of quantization:
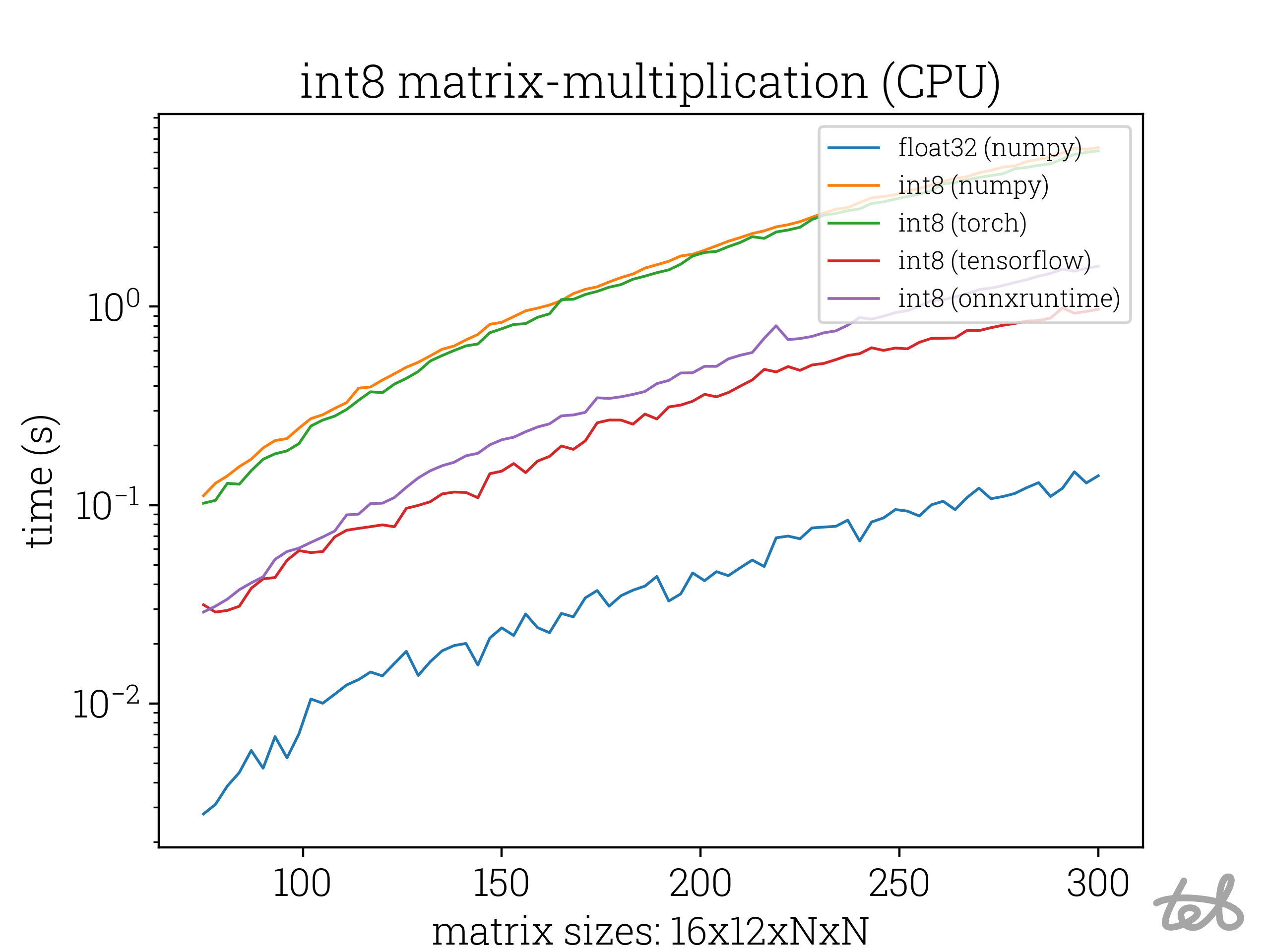Runtime Analysis of the int8 matrix-matrix multiplication of two identical matrices for differing values of N. In the case of
int8-integers the accumulation is performed with int32-integers.
Well, there are all better than numpy, but one would think that int8 matrix-matrix multiplication should be actually
faster than float32 matrix-matrix multiplication.
A convenient problem solver: oneDNN
It seems like there's no pip install-ready solution available. Since my Laptop's got an Intel CPU, I decided to give their framework
oneDNN for neural network acceleration a try.
The approach immediately proved itself. Starting from the provided example for matrix multiplication, 34 lines of C++ do the Job:
#include "dnnl.hpp"
#include "matmul.h"
void int8_matmul(int8_t* A, int8_t* B, int32_t* C, int64_t D1, int64_t D2, int64_t M, int64_t K, int64_t N) {
dnnl::engine eng(dnnl::engine::kind::cpu, 0);
// Create a MatMul primitive descriptor for the following op: C_u32 = A_u8 * B_u8
const int64_t d_D1 = DNNL_RUNTIME_DIM_VAL;
const int64_t d_D2 = DNNL_RUNTIME_DIM_VAL;
const int64_t d_M = DNNL_RUNTIME_DIM_VAL;
const int64_t d_K = DNNL_RUNTIME_DIM_VAL;
const int64_t d_N = DNNL_RUNTIME_DIM_VAL;
dnnl::memory::desc a_md({d_D1, d_D2, d_M, d_K}, dnnl::memory::data_type::s8, dnnl::memory::format_tag::abcd);
dnnl::memory::desc b_md({d_D1, d_D2, d_K, d_N}, dnnl::memory::data_type::s8, dnnl::memory::format_tag::abcd);
dnnl::memory::desc c_md({d_D1, d_D2, d_M, d_N}, dnnl::memory::data_type::s32, dnnl::memory::format_tag::abcd);
dnnl::matmul::primitive_desc matmul_pd = dnnl::matmul::primitive_desc(eng, a_md, b_md, c_md);
// Create Matmul Primitive
dnnl::matmul matmul_p(matmul_pd);
// Create memory objects at the locations given by A, B and C
dnnl::memory A_s8_mem({{D1, D2, M, K}, dnnl::memory::data_type::s8, dnnl::memory::format_tag::abcd}, eng, A);
dnnl::memory B_s8_mem({{D1, D2, K, N}, dnnl::memory::data_type::s8, dnnl::memory::format_tag::abcd}, eng, B);
dnnl::memory C_s32_mem({{D1, D2, M, N}, dnnl::memory::data_type::s32, dnnl::memory::format_tag::abcd}, eng, C);
// Execute the MatMul primitive
dnnl::stream s(eng);
matmul_p.execute(s,
{{DNNL_ARG_SRC, A_s8_mem},
{DNNL_ARG_WEIGHTS, B_s8_mem},
{DNNL_ARG_DST, C_s32_mem}});
s.wait();
}
Adding some manageable boilerplate makes this available in python. Simply compile int8_matmul with C linkage:
#ifndef MATMUL_H
#define MATMUL_H
#include <stdint.h>
int main(int argc, char **argv);
extern "C" {
void int8_matmul(int8_t* A, int8_t* B, int32_t* C, int64_t D1, int64_t D2, int64_t M, int64_t K, int64_t N);
} //end extern "C"
#endif // MATMUL_H
And call it in python via the foreign function interface:
from cffi import FFI
import numpy as np
import numpy_int_ops_cpu
# Instantiate FFI
dllURI = f"{numpy_int_ops_cpu.__path__[0]}/libIntOps.so"
funDef = """
void int8_matmul(int8_t* A, int8_t* B, int32_t* C, int64_t D1, int64_t D2, int64_t M, int64_t K, int64_t N);
"""
ffi = FFI()
cpp_lib = ffi.dlopen(dllURI)
ffi.cdef(funDef)
def get_pointer_to_np_arr(arr, ctype, ffi):
return ffi.cast(ctype, arr.ctypes.data)
def int8_matmul(A: np.ndarray[None, np.int8], B: np.ndarray[None, np.int8]) -> np.ndarray[None, np.int32]:
assert A.dtype == np.int8, "A must be int8"
assert B.dtype == np.int8, "B must be int8"
assert len(A.shape) == 4, "A must be 4D tensor"
assert len(B.shape) == 4, "B must be 4D tensor"
assert A.shape[:-4] == B.shape[:-4], f"Cannot matmul A (shape={A.shape}) and B (shape={B.shape})"
assert A.shape[:-3] == B.shape[:-3], f"Cannot matmul A (shape={A.shape}) and B (shape={B.shape})"
assert A.shape[-1] == B.shape[-2], f"Cannot matmul A (shape={A.shape}) and B (shape={B.shape})"
D1 = A.shape[-4]
D2 = A.shape[-3]
K, M, N = A.shape[-2], A.shape[-1], B.shape[-1]
C = np.empty(shape=(D1, D2, K, N), dtype=np.int32)
A_pointer = get_pointer_to_np_arr(A, "int8_t*", ffi)
B_pointer = get_pointer_to_np_arr(B, "int8_t*", ffi)
C_pointer = get_pointer_to_np_arr(C, "int32_t*", ffi)
cpp_lib.int8_matmul(A_pointer, B_pointer, C_pointer, D1, D2, K, M, N)
return C
That's it!
Conclusion
Rerunning the runtime analysis from above shows:
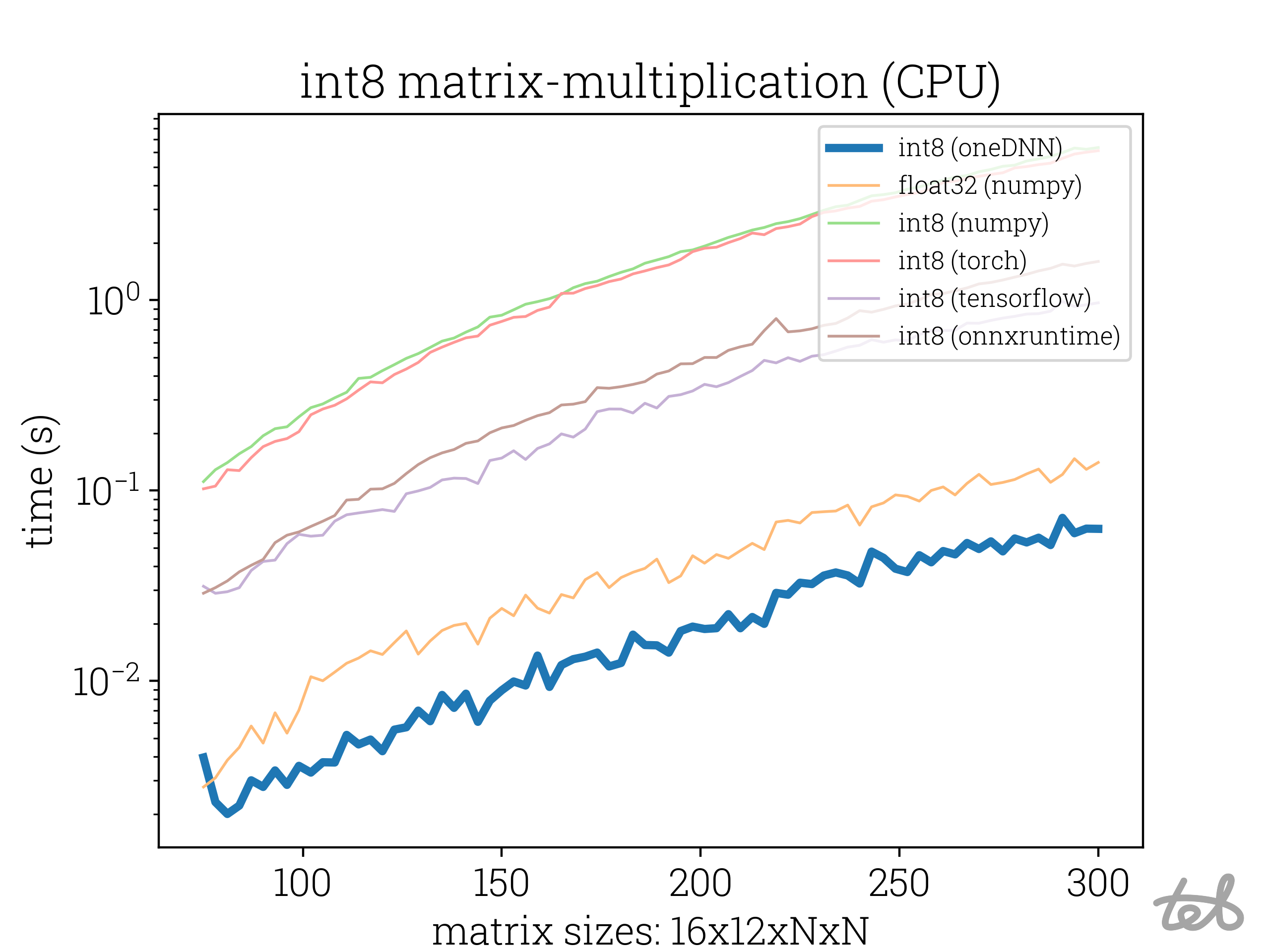Runtime Analysis for different int8 matrix multiplication methods including the custom oneDNN based implentation. Performance
for float32 included for comparison.
int8-matrix-multiplication (with int32-accumulation) is now a lot faster than float32-matrix-multiplication. Neat.
For a complete implementation of the shown code, see my GitHub Repo numpy-int-ops.
