Home

Quantizing Transformers

Tilmann E. Bartsch, 21.05.2023

The model size and computational costs of modern neural networks are huge. Both can be significantly reduced by using a method called quantization. This post is a detailed guide on how to quantize neural networks and will build up everything required to perform a simple quantization of Google's transformer-based ViT from scratch.

If you only want to see the code:

 

Table of Contents

Intro: From quantizing an MLP to quantizing ViT

Quantizing transformers shows to improve memory usage and inference speed by up to four times - maybe even more then that in the futre. As transformers have become ubiquitous in current advances in the machine learning domain a lot of folks started working on quantizing them. I.e. this, this, this, this and this paper have been published in last few months.

If you are developing transformer architectures and care about inference cost then you should consider how to quantize your networks. Unfortunately, existing tools like Google's tensorflow-lite, Facebook's quantization API or Qualcomm's aimet are complex tools looking like black-boxes from the outside.

Quantization is actually very simple when removing all boilerplate. In part I of this post a ~100 line standalone MLP quantization script (source) using only numpy will be developed which quantizes a simple MLP trained on a circles dataset.

As an appetizer: the effect of quantization for the MLP trained on a circles dataset can be visualized like this:

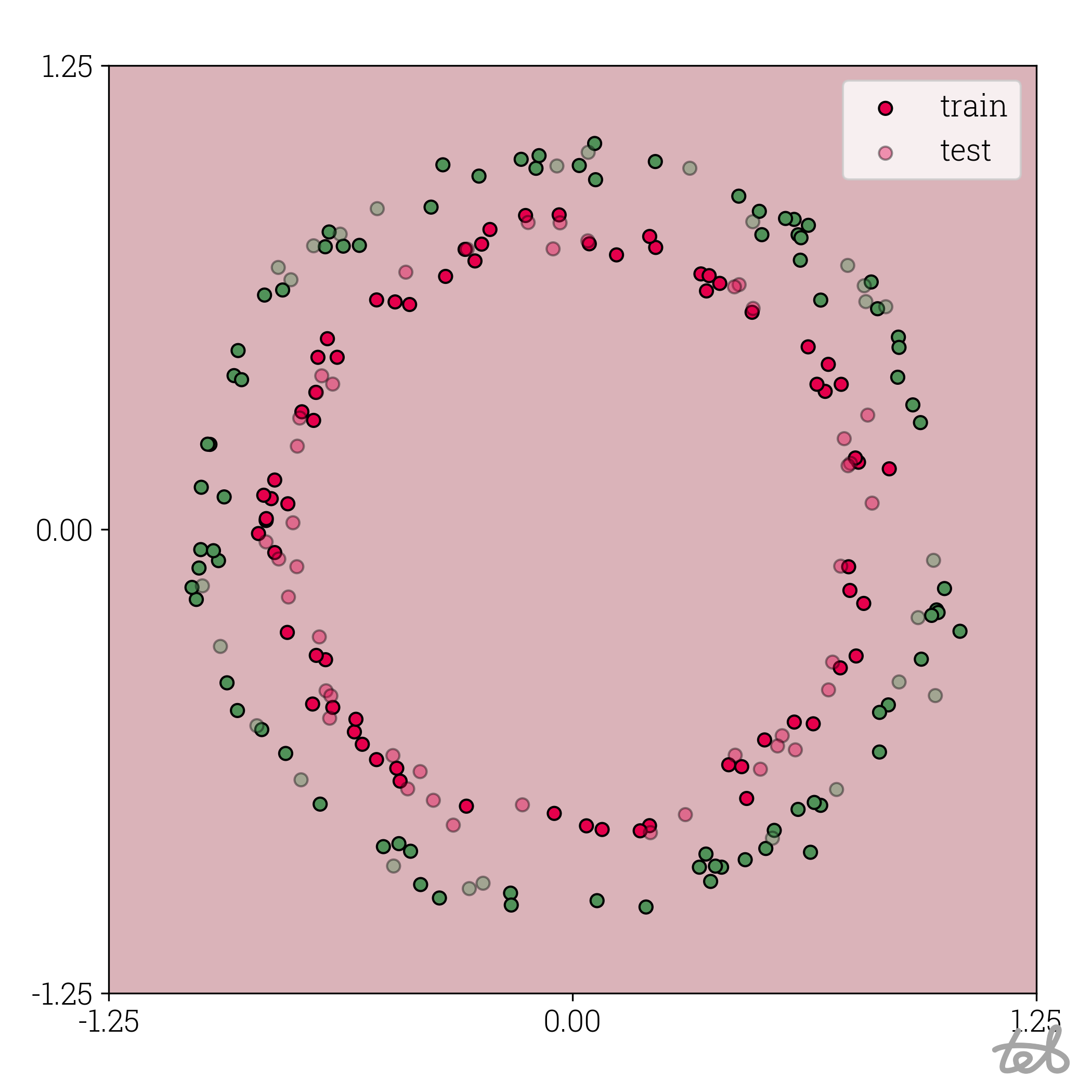Circle dataset with 1-bit quantized MLP contour plot 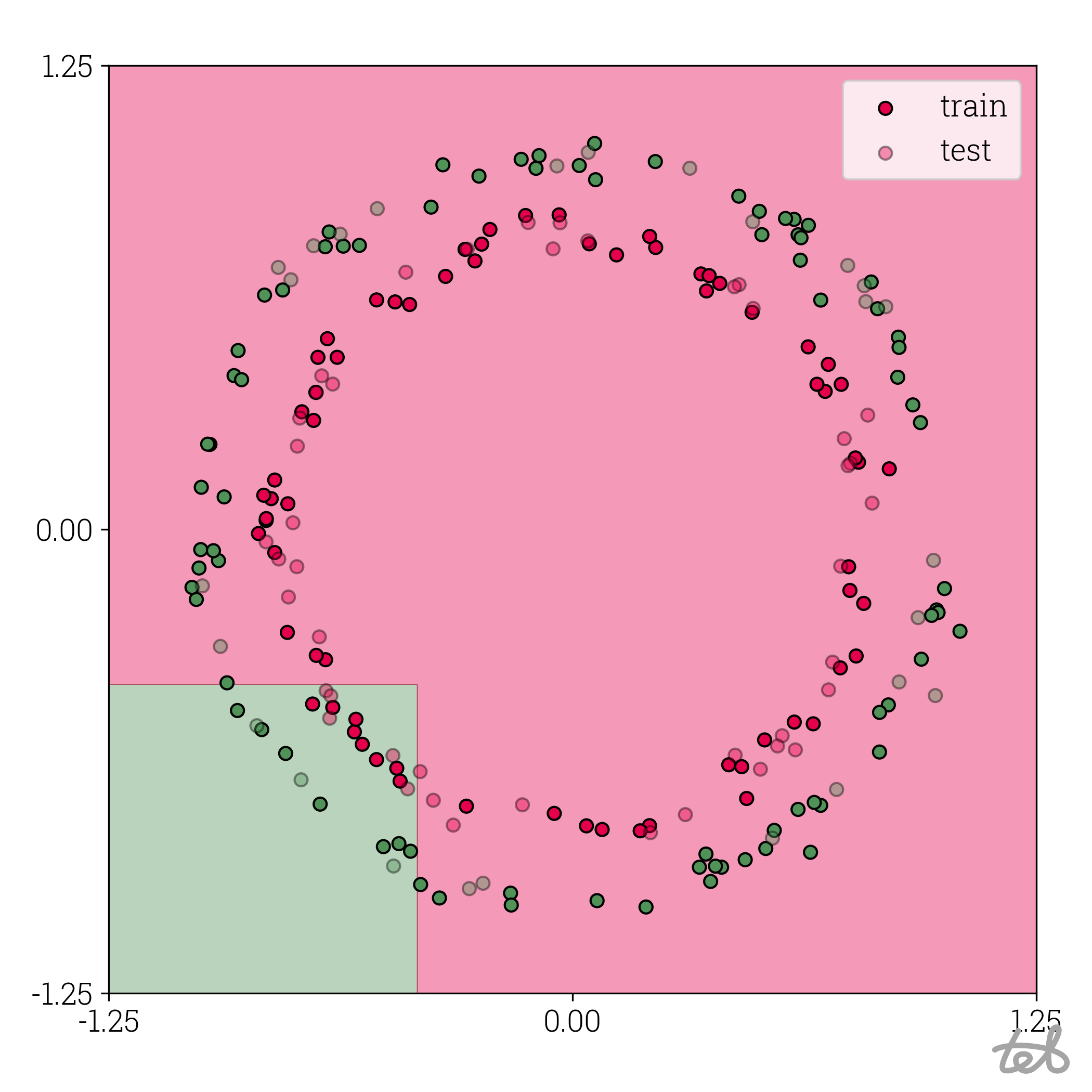Circle dataset with 1-bit quantized MLP contour plot

Circle dataset with 2-bit quantized MLP contour plot Circle dataset with 2-bit quantized MLP contour plot

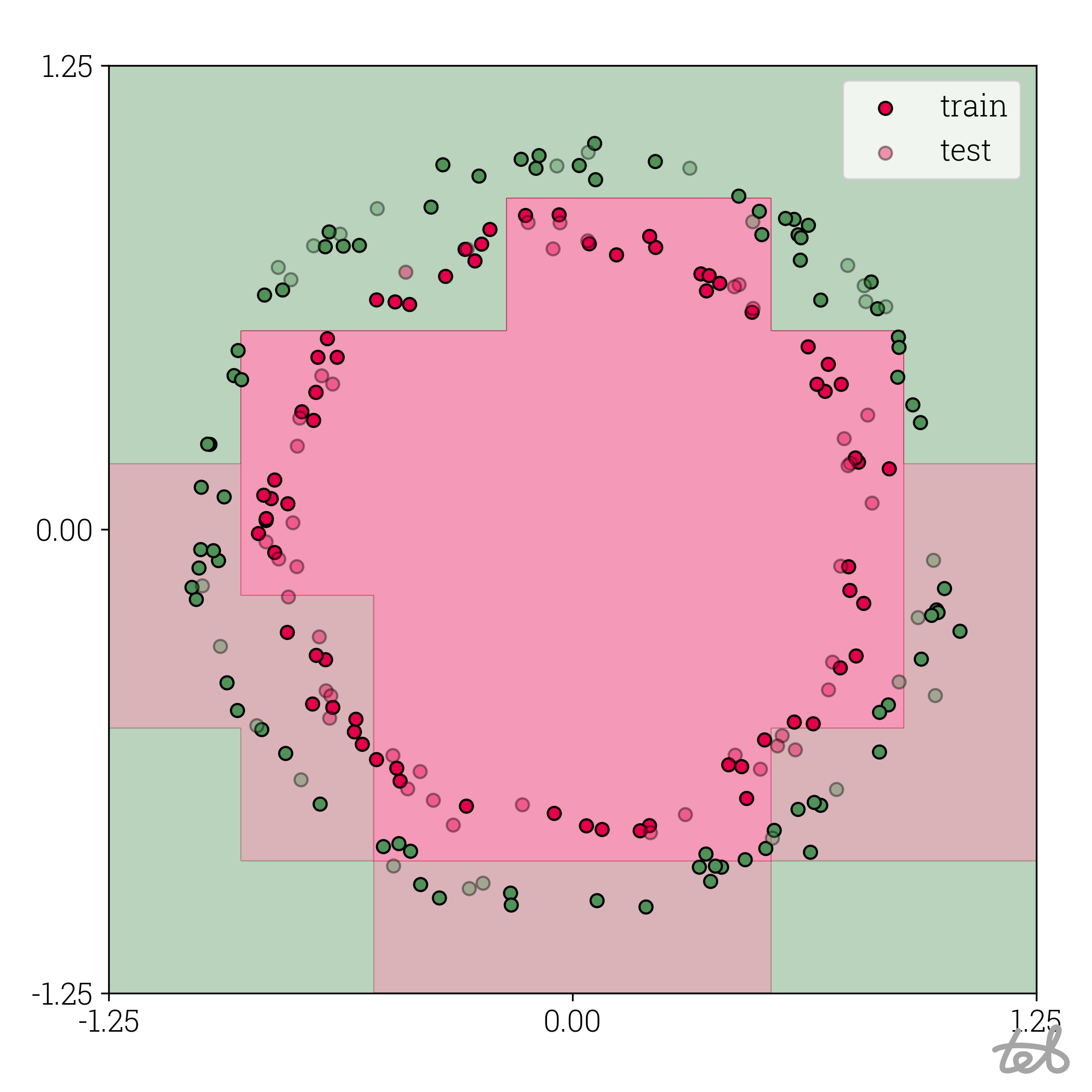Circle dataset with 3-bit quantized MLP contour plot Circle dataset with 3-bit quantized MLP contour plot

Circle dataset with 4-bit quantized MLP contour plot Circle dataset with 4-bit quantized MLP contour plot

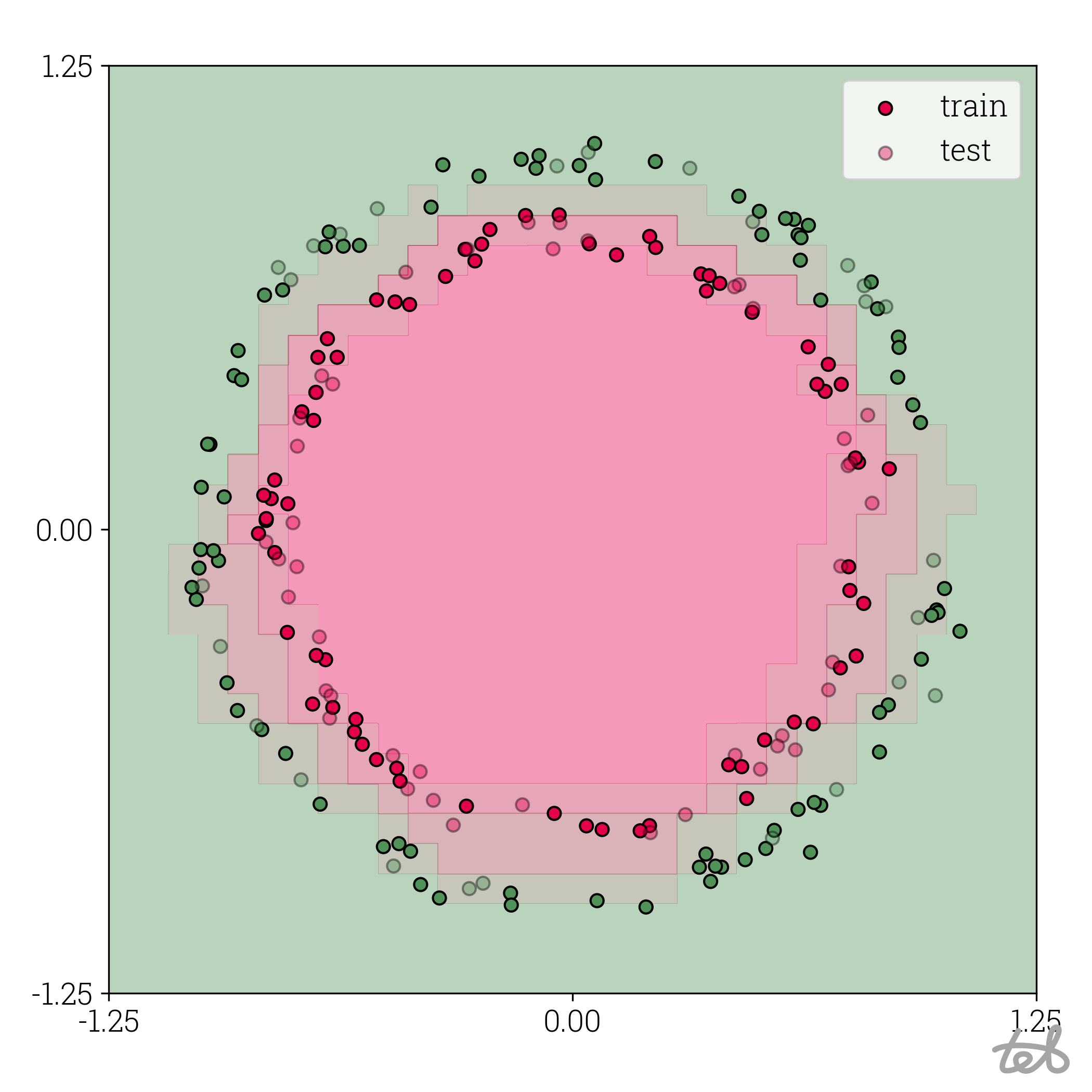Circle dataset with 5-bit quantized MLP contour plot Circle dataset with 5-bit quantized MLP contour plot

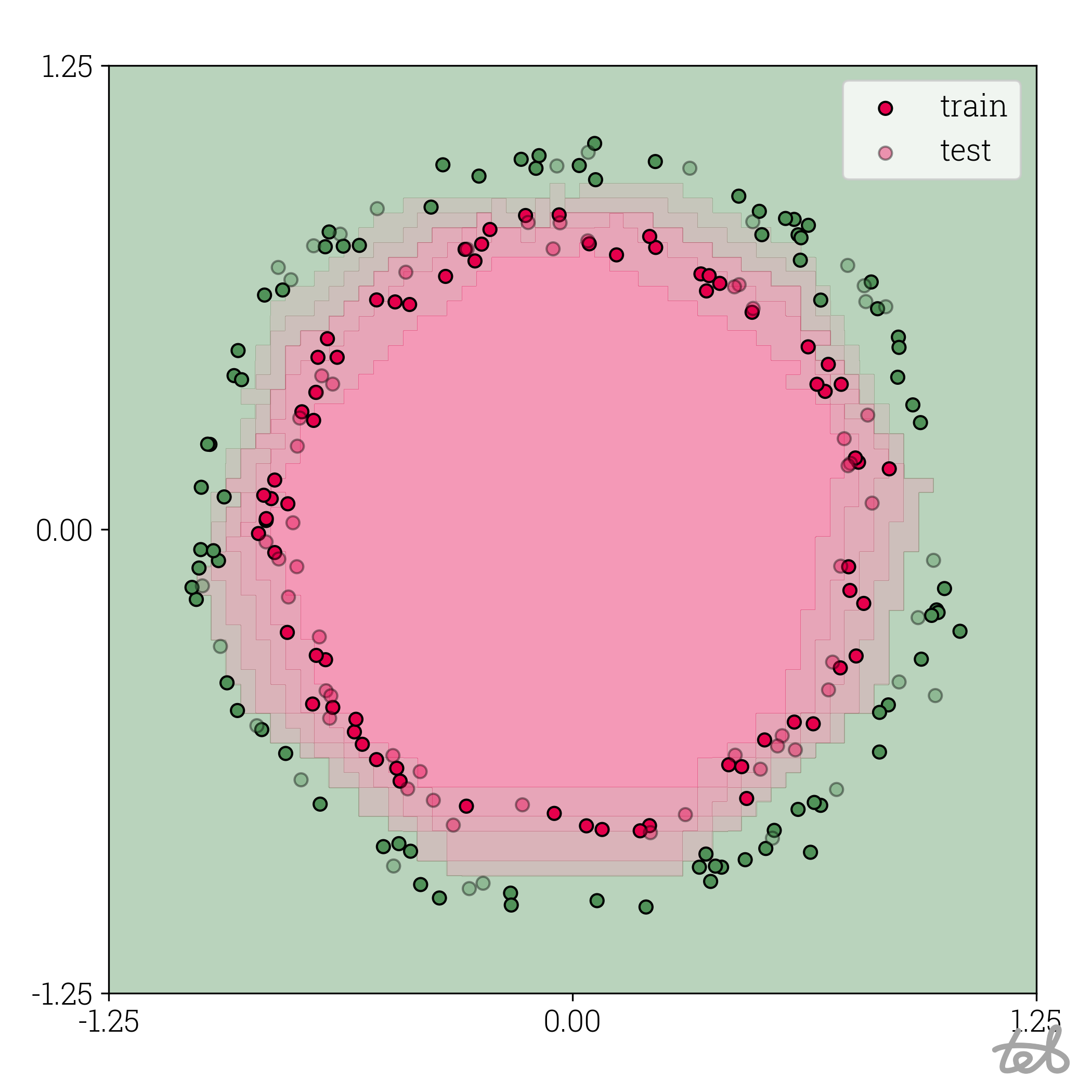Circle dataset with 6-bit quantized MLP contour plot Circle dataset with 6-bit quantized MLP contour plot

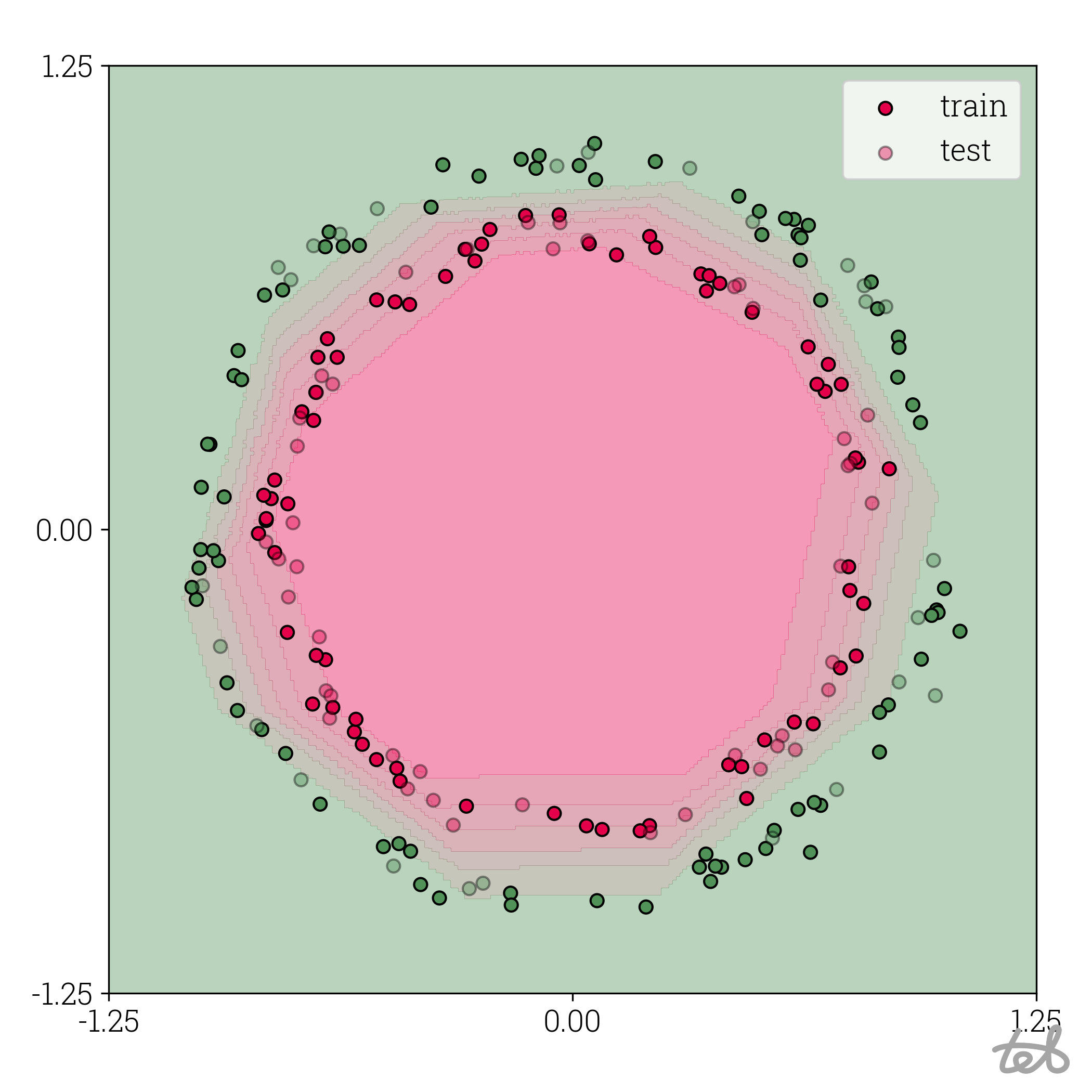Circle dataset with 8-bit quantized MLP contour plot Circle dataset with 8-bit quantized MLP contour plot

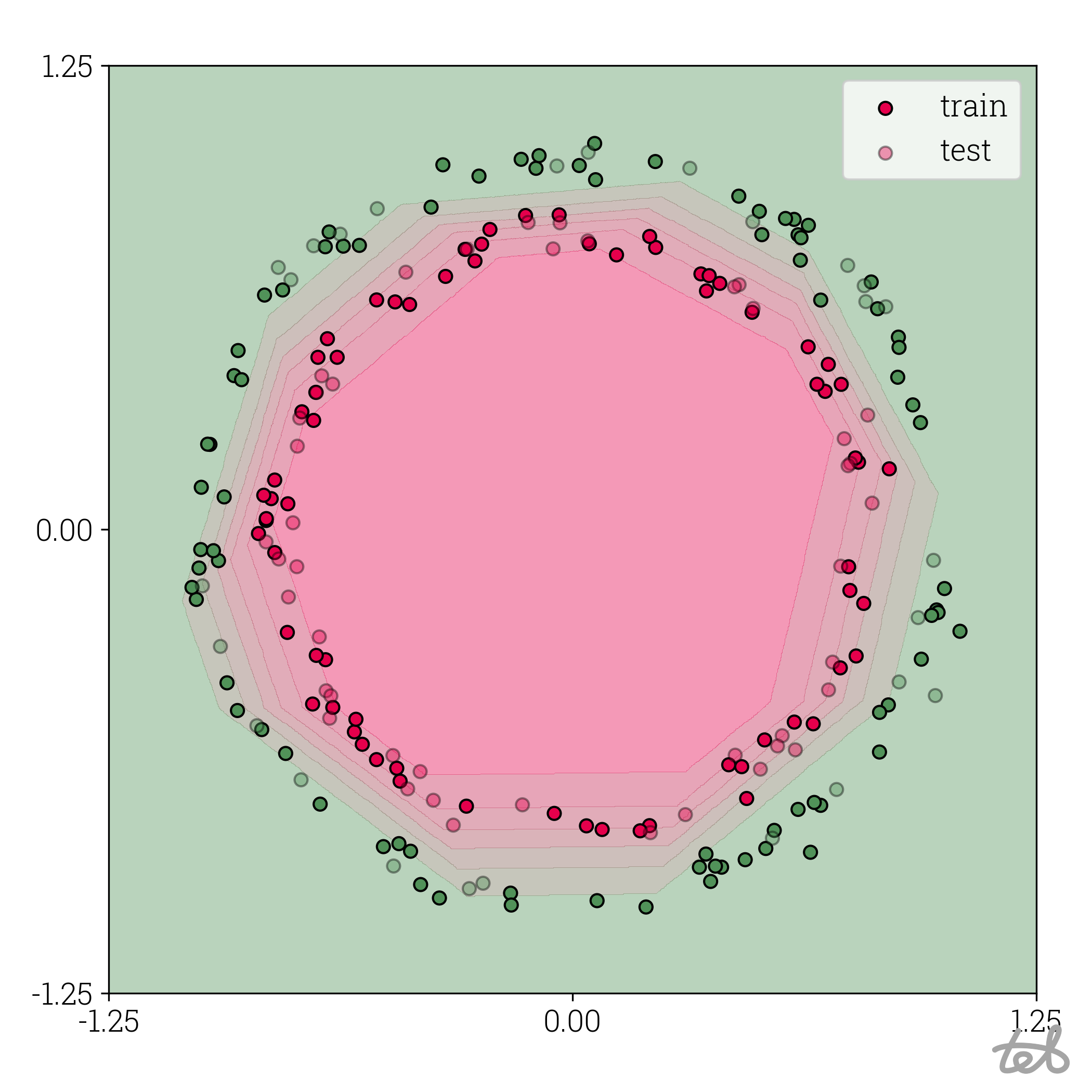Circle dataset with 10-bit quantized MLP contour plot Circle dataset with 10-bit quantized MLP contour plot

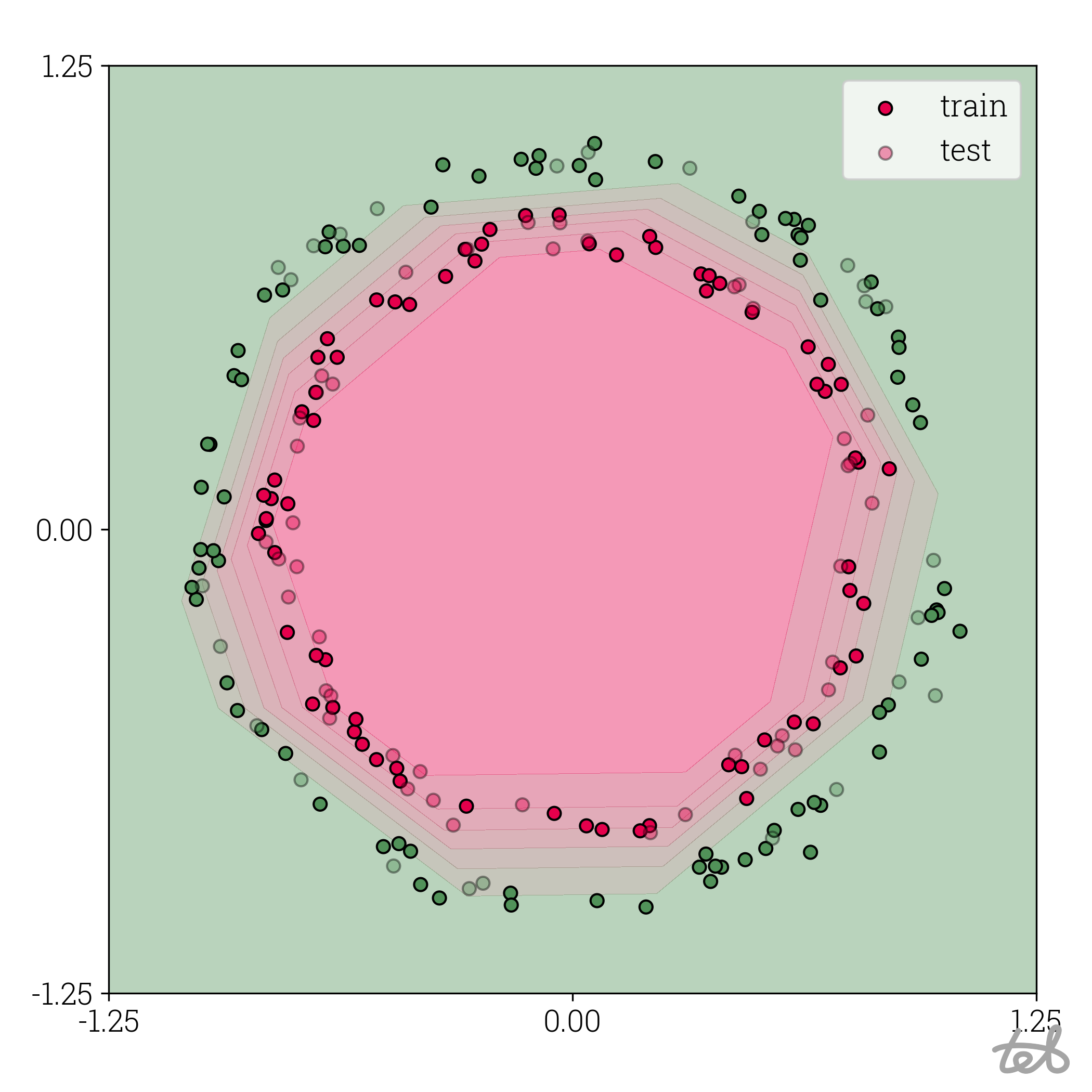Circle dataset with float32 MLP contour plot Circle dataset with f32 MLP contour plot

Part II will show how to use this idea to build a simplistic quantization framework able to quantize ViT.

Part I: Quantizing an MLP in 120 lines of code

In this part, we will develop a python script which quantizes a multi-layer-perceptron (MLP) in <120 lines of code using only numpy. For that, we follow three steps:

By covering the quantization of (general) matrix-matrix multiplication, we are able to quantize dense layers as well as matrix-mulitplication-layers enabling to quantize ViT in Part II.

All code snippets in this part are designed to work isolated. They are meant to be executed and played with while reading this post. Don't be discouraged by the increasing size of the snippets. Only a few lines of new code is added in every listing.

A simple start: Quantizing tensors

Quantizing a tensor is a straightforward endeavor. I.e. for int8-quantization it corresponds to rescaling and round the float32 values of a tensor to integers between -128 to 127 represented by int8-numbers.

More formally, we can consider a tensor x\in\mathbb{R}^{m\times n} and aim to represent x by a tensor q_x\in\lbrace-2^k,\dots,2^k-1\rbrace (k representing the bit width), a zero point z_x\in\lbrace-2^k,\dots,2^k-1\rbrace and a scale s_x\in\mathbb{R} such that:

\label{eqn:tensor_quantization} x \approx (q_x - z_x) \cdot s_x \tag{1}

For given s_x and z_x we can compute (\lfloor.\rceil denotes rounding to the nearest integer)

q_x = \left\lfloor z_x + \frac{1}{s_x}\cdot x\right\rceil

and test the quantization error by inserting the resulting q_x into \eqref{eqn:tensor_quantization}.

A numpy implementation of this can be done like so:

import numpy as np

arr = np.array([[ 4.4037123 ], [-2.9683902 ], [-4.4077654 ], [ 2.3313837 ], [ 0.05330967]], dtype=np.float32)

def quantize(data: np.ndarray, scale: float, zero_point: int, bit_width: int):
    q_data = zero_point + data / scale

    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    # Rescaled numbers which are smaller than the minimum quantized value `min_qval` are clipped to
    # this minimum value. Analogously for rescaled numbers greater than `max_qval`.
    q_data_clipped = np.clip(q_data, min_qval, max_qval)  
    q_data_boxed = np.array(np.rint(q_data_clipped), dtype=np.int64)

    return q_data_boxed

def dequantize(arr: np.ndarray, scale: float, zero_point: int | np.ndarray):
    return ((arr - zero_point) * scale).astype(np.float32)

# We choose scaling parameters which rescale the data approximately to an interval of -128 to 127
scale = 0.04
zero_point = 0

arr_quantized = quantize(arr, scale, zero_point, bit_width=8)
arr_round_trip = dequantize(arr_quantized, scale, zero_point)

with np.printoptions(precision=4, suppress=True):
    print("arr:\n", np.array2string(arr))
    print("arr_quantized:\n", np.array2string(arr_quantized))
    print("arr_round_trip:\n", np.array2string(arr_round_trip))
    print("round-trip error:\n", np.abs(arr - arr_round_trip))

The code above yields the following result, in which we observe that the quantization/dequantization round-trip error is ~1%.

f32 origin int8 quantized f32 round-tripped round-trip error
4.4037 110 4.4000 0.0037
-2.9684 -74 -2.9600 0.0084
-4.4078 -110 -4.4000 0.0078
2.3314 58 2.3200 0.0114
0.0533 1 0.0400 0.0133

In the current code the scale and zero_point are chosen arbitrarily. The easiest way to obtain those parameters is using the tensor's minimum and maximum value. This procedure can be found in the function quant_parameters below, which implements two quantization modes, namely

import numpy as np

arr = np.array([[ 4.4037123 ], [-2.9683902 ], [-4.4077654 ], [ 2.3313837 ], [ 0.05330967]], dtype=np.float32)

def quantize(data: np.ndarray, scale: float, zero_point: int, bit_width: int):
    q_data = zero_point + data / scale

    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    # Rescaled numbers which are smaller than the minimum quantized value `min_qval` are clipped to
    # this minimum value. Analogously for rescaled numbers greater than `max_qval`.
    q_data_clipped = np.clip(q_data, min_qval, max_qval)  
    q_data_boxed = np.array(np.rint(q_data_clipped), dtype=np.int64)

    return q_data_boxed

def dequantize(arr: np.ndarray, scale: float, zero_point: int | np.ndarray):
    return ((arr - zero_point) * scale).astype(np.float32)

def quant_parameters(min_val: np.float32, max_val: np.float32, bit_width: int, asymmetric: bool):
    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0

    if asymmetric:
        scale = (max_val - min_val) / (max_qval - min_qval)
        zero_point0 = min_qval - min_val / scale
        zero_point = np.rint(zero_point0).astype(np.int64)
    else:
        scale = (2 * max(max_val, min_val)) / (max_qval - min_qval)
        zero_point = np.array(0, np.int64)

    return scale, zero_point

scale, zero_point = quant_parameters(arr.min(), arr.max(), bit_width=8, asymmetric=True)

arr_quantized = quantize(arr, scale, zero_point, bit_width=8)
arr_round_trip = dequantize(arr_quantized, scale, zero_point)

with np.printoptions(precision=4, suppress=True):
    print(f"scale = {scale}, zero_point = {zero_point}")
    print("arr:\n", np.array2string(arr))
    print("arr_quantized:\n", np.array2string(arr_quantized))
    print("arr_round_trip:\n", np.array2string(arr_round_trip))
    print("round-trip error:\n", np.abs(arr - arr_round_trip))

This code calculates scale == 0.0346, zero_point == 0 as well as a table similar to the one above.

Repeating the procedure for varying bit widths by adjusting the corresponding parameter in the script allows to compare the quantization error for different quantization intensities:

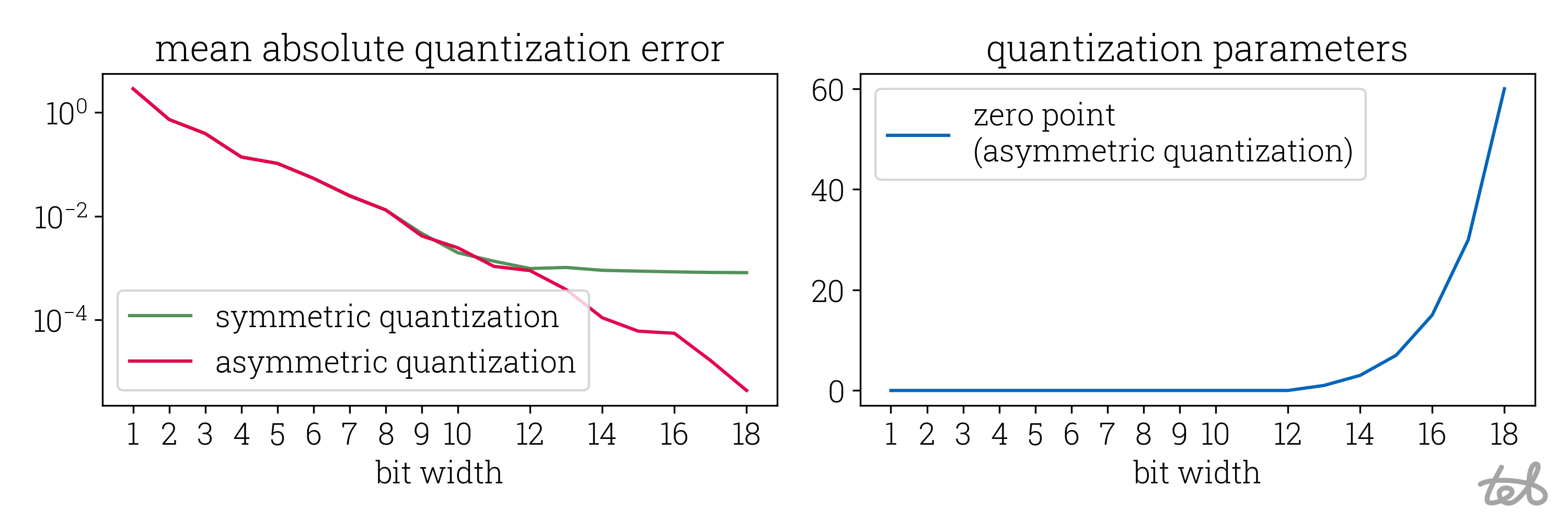Graph showing the mean absolute quantization error of an example tensor as well as the used zero point for different bit widths This plot shows the quantization/dequantization round-trip error for the tensor [4.4, -3.0, -4.4, 2.3, 0.0] as defined in the script above as well as the corresponding zero point used in asymmetric quantization. The error decreases exponentially with respect to the used bit width. Note that the mean absolute error of the symmetric quantization saturates around a bit width of 12 which corresponds to the bit width at which a zero point unequal to zero is used in asymmetric quantization.

This tells us nothing about the quality of quantization yet because in the end the accuracy drop of a complete network is the only relevant parameter. We'll come back to that later.

Note:
The rescaling operation could be formulated in different manners as well, i.e. scale * (zero_point + data). See gemmlowp's quantization tutorial for details why these alternatives are not used.

Into the rabbit hole: Quantizing a matrix-matrix multiplication

Before implementing quantized matrix-matrix multiplication we formulate the basic idea as has been done in Benoit et al.'s quantization paper.

For floating point tensors, x_1\in\mathbb{R}^{k\times m} and x_2\in\mathbb{R}^{m\times n} and their matrix multiplication w=x_1\cdot x_2 we write similar to above

x_1 \approx (q_{x_1} - z_{x_1}) \cdot s_{x_1} \\ x_2 \approx (q_{x_2} - z_{x_2}) \cdot s_{x_2} \\ w \approx (q_w - z_w) \cdot s_w

Now since w=x_1\cdot x_2 we can assume

\label{eqn:matmul_quantization_start_point} (q_w - z_w) \cdot s_w \approx ((q_{x_1} - z_{x_1}) \cdot s_{x_1}) \cdot ((q_{x_2} - z_{x_2}) \cdot s_{x_2}) \tag{2}

Which can be rearranged to

\label{eqn:quantized_matmul} q_w \approx z_w + \frac{1}{s_w}\underbrace{s_{x_1}s_{x_2}}_{:=s_y} (\underbrace{q_{x_1}q_{x_2}}_{:=q_y} \underbrace{-z_{x_1}q_{x_2}-z_{x_2}q_{x_1}+z_{x_1}z_{x_2}}_{:=z_y}) \tag{3}

Be aware of the sloppy notation used in the terms z_{x_1}q_{x_2} and z_{x_2}q_{x_1} and z_{x_1}z_{x_2}: i.e. z_{x_1} has to be considered as a matrix of shape x_1 with the element z_{x_1} at each position.

Before implementing this, we divide \eqref{eqn:quantized_matmul} into two parts:

  1. Calculate q_y, s_y and z_y. This is called quantized matrix-matrix multiplication. Note that

    • q_y requires a higher bit-width to represent than q_{x_1} and q_{x_2}. Otherwise, an overflow would occur very easily. The common approach is to represent q_{x_1} and q_{x_2} width 8 bits and q_y with 32 bits.
    • the zero point z_y is actually a matrix of the same shape as q_y.

  2. Calculate (\lfloor.\rceil denotes rounding to the nearest integer)

    \qquad q_w = \left\lfloor z_w + \frac{s_y}{s_w}\cdot(q_y - z_y)\right\rceil

    This step is called requantization.

We proceed by baking these formulas into another standalone script.

import numpy as np

x1 = np.array([[-0.68969274,  0.36898366], [ 0.48721004,  0.59565425], [ 0.9734074 , -0.08323386]], dtype=np.float32)
x2 = np.array([[ 4.4037123 , -2.9683902 , -4.4077654 ,  2.3313837 ,  0.05330967], [-1.0420023 ,  3.5323772 , -1.5059234 ,  4.3279686 , -4.243471  ]], dtype=np.float32)

def quantize(data: np.ndarray, scale: float, zero_point: int, bit_width: int):
    q_data = zero_point + data / scale

    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    # Rescaled numbers which are smaller than the minimum quantized value `min_qval` are clipped to
    # this minimum value. Analogously for rescaled numbers greater than `max_qval`.
    q_data_clipped = np.clip(q_data, min_qval, max_qval)  
    q_data_boxed = np.array(np.rint(q_data_clipped), dtype=np.int64)

    return q_data_boxed

def dequantize(arr: np.ndarray, scale: float, zero_point: int | np.ndarray):
    return ((arr - zero_point) * scale).astype(np.float32)

def quant_parameters(min_val: np.float32, max_val: np.float32, bit_width: int, asymmetric: bool):
    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0

    if asymmetric:
        scale = (max_val - min_val) / (max_qval - min_qval)
        zero_point0 = min_qval - min_val / scale
        zero_point = np.rint(zero_point0).astype(np.int64)
    else:
        scale = (2 * max(max_val, min_val)) / (max_qval - min_qval)
        zero_point = np.array(0, np.int64)

    return scale, zero_point

def q_matmul(arr_a: np.ndarray, scale_a: float, zero_point_a: int,
           arr_b: np.ndarray, scale_b: float, zero_point_b: int):
    q_matmul_result = np.matmul(arr_a.astype(np.int64), arr_b)
    scale = scale_a * scale_b
    zero_points = (arr_a.sum(axis=-1, keepdims=True) * zero_point_b
                  + arr_b.sum(axis=-2, keepdims=True) * zero_point_a
                  - zero_point_a * zero_point_b * arr_a.shape[-1])
    return q_matmul_result, scale, zero_points

def requantize(arr: np.ndarray, arr_scale: float, arr_zero_points: np.ndarray,
               res_scale: float, res_zero_point: int, bit_width: int):
    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    dequant = dequantize(arr, arr_scale, arr_zero_points)
    qdata = np.clip(np.rint(res_zero_point + 1 / res_scale * dequant), min_qval, max_qval).astype(np.int64)
    return qdata

# Float matrix multiplication
w_f32 = np.matmul(x1, x2)

# Quantize input arrays
x1_scale, x1_zero_point = quant_parameters(x1.min(), x1.max(), bit_width=8, asymmetric=True)
x2_scale, x2_zero_point = quant_parameters(x2.min(), x2.max(), bit_width=8, asymmetric=True)
x1_quant = quantize(x1, x1_scale, x1_zero_point, bit_width=8)
x2_quant = quantize(x2, x2_scale, x2_zero_point, bit_width=8)

# Perform matrix multiplication. Result is quantized with a higher bit width, i.e. for `bit_width == 8`
# the elements of result `q_mm` have a bit_width of 32.
y, y_scale, y_zero_points = q_matmul(x1_quant, x1_scale, x1_zero_point, x2_quant, x2_scale, x2_zero_point)

# Requantize to original bit_width, i.e. 8. For that use quantization parameters obtained from `f32_matmul`.
w_scale, w_zero_point = quant_parameters(w_f32.min(), w_f32.max(), bit_width=8, asymmetric=True)
w_quant = requantize(y, y_scale, y_zero_points,
                     w_scale, w_zero_point, bit_width=8)

# Dequantize result
w_round_trip = dequantize(w_quant, w_scale, w_zero_point)

with np.printoptions(precision=4, suppress=True):
    print("w_f32:\n", np.array2string(w_f32))
    print("w_round_trip:\n", np.array2string(w_round_trip))
    print("round-trip error:\n", np.abs(w_f32 - w_round_trip))

which prints the following three (3x5)-arrays:

f32 matmul quantized matmul error
-3.4217 3.3507 2.4843 -0.0110 -1.6025 -3.4154 3.3484 2.4779 0.0000 -1.6407 0.0063 0.0022 0.0065 0.0110 0.0382
1.5249 0.6578 -3.0445 3.7138 -2.5017 1.5403 0.6362 -3.0806 3.6833 -2.4779 0.0154 0.0216 0.0361 0.0306 0.0238
4.3733 -3.1835 -4.1652 1.9092 0.4051 4.3530 -3.1810 -4.1521 1.8751 0.4353 0.0204 0.0024 0.0131 0.0340 0.0302

Like above, we can compare the approximation quality:

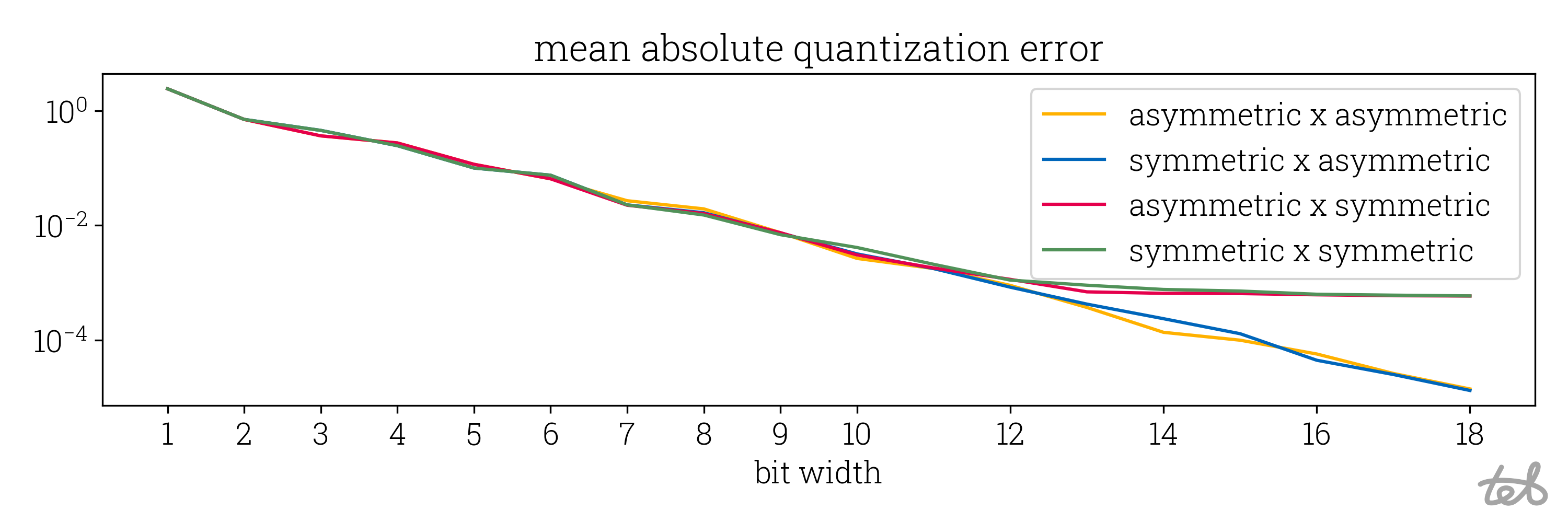Graph showing the mean absolute quantization error of a quantized matrix-matrix multiplication Mean absolute quantization error of the quantized matrix-matrix multiplication as implemented in the code above. Each combination of symmetric/asymmetric quantization of the input matrix is evaluated. The error reduces exponentially with the bit width and saturates around a bit width of 13 if the second matrix is quantized symmetrically.

Stringing it together: Obtaining an MLP's quantization accuracy drop

We finalize the first part by quantizing a very simple MLP with a single hidden layer, which is trained on a non-linear circles-dataset. See this file for the exact model definition and training procedure.

In the following image, we can see the utilized dataset containing of x- and y-locations as features and one of two classes (green or red) as label/target. Furthermore, the trained model is evaluated on a close-meshed grid to obtain a contour plot:

Visualization of circle dataset with 2 classes and a corresponding contour plot of a trained MLP Visualization of circle dataset with two classes. The features are the x and y position of every dot and the color corresponds to one of the two possible targets/labels. In the background the contour plot of an MLP trained on this dataset is shown.

Before we are able to quantize this MLP, we have to adjust our current formula derived from \eqref{eqn:matmul_quantization_start_point} to support bias. For that we denote x_1\in\mathbb{R}^{k\times m}, x_2\in\mathbb{R}^{m\times n} and b\in\mathbb{R}^{k\times n} and general matrix multiplication w=x_1\cdot x_2 + b. Using the notation from above, we obtain

q_w \approx z_w + \frac{1}{s_w}s_{x_1}s_{x_2}(q_{x_1}q_{x_2}-z_{x_1}q_{x_2}-z_{x_2}q_{x_1}+z_{x_1}z_{x_2} + \frac{b}{s_{x_1}s_{x_2}})

Which means that we can support a bias in the quantized matrix multiplication by

  1. Quantizing b to q_b with scale s_{x_1}s_{x_2} and zero point 0 such that

    \qquad b \approx s_{x_1}s_{x_2}\cdot q_b

  2. Performing quantized general matrix-matrix multiplication by calculating q_y=q_{x_1}q_{x_2}+q_b as well as s_y=s_{x_1}s_{x_2} and z_y=-z_{x_1}q_{x_2}-z_{x_2}q_{x_1}+z_{x_1}z_{x_2}.

  3. Requantize the result the same way as before by calculating

    \qquad q_w = \left\lfloor z_w + \frac{s_y}{s_w}\cdot(q_y - z_y)\right\rceil

Writing everything down, we get an MLP quantization script containing less than 120 lines of code:

import numpy as np

# Quantization routines

def quantize(data: np.ndarray, scale: float, zero_point: int, bit_width: int):
    q_data = zero_point + data / scale

    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    # Rescaled numbers which are smaller than the minimum quantized value `min_qval` are clipped to
    # this minimum value. Analogously for rescaled numbers greater than `max_qval`.
    q_data_clipped = np.clip(q_data, min_qval, max_qval)  
    q_data_boxed = np.array(np.rint(q_data_clipped), dtype=np.int64)

    return q_data_boxed

def dequantize(arr: np.ndarray, scale: float, zero_point: int | np.ndarray):
    return ((arr - zero_point) * scale).astype(np.float32)

def quant_parameters(min_val: np.float32, max_val: np.float32, bit_width: int, asymmetric: bool):
    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0

    if asymmetric:
        scale = (max_val - min_val) / (max_qval - min_qval)
        zero_point0 = min_qval - min_val / scale
        zero_point = np.rint(zero_point0).astype(np.int64)
    else:
        scale = (2 * max(max_val, min_val)) / (max_qval - min_qval)
        zero_point = np.array(0, np.int64)

    return scale, zero_point

def q_matmul(arr_a: np.ndarray, scale_a: float, zero_point_a: int,
           arr_b: np.ndarray, scale_b: float, zero_point_b: int):
    q_matmul_result = np.matmul(arr_a.astype(np.int64), arr_b)
    scale = scale_a * scale_b
    zero_points = (arr_a.sum(axis=-1, keepdims=True) * zero_point_b
                  + arr_b.sum(axis=-2, keepdims=True) * zero_point_a
                  - zero_point_a * zero_point_b * arr_a.shape[-1])
    return q_matmul_result, scale, zero_points

def requantize(arr: np.ndarray, arr_scale: float, arr_zero_points: np.ndarray,
               res_scale: float, res_zero_point: int, bit_width: int):
    min_qval, max_qval = -2.0 ** (bit_width - 1), 2.0 ** (bit_width - 1) - 1.0
    dequant = dequantize(arr, arr_scale, arr_zero_points)
    qdata = np.clip(np.rint(res_zero_point + 1 / res_scale * dequant), min_qval, max_qval).astype(np.int64)
    return qdata

# Trained MLP for circles dataset

# # Every row of `inp` contains the x and y position of a point
inp = np.array([[0., 0.], [1., 1.]], dtype=np.float32) 

fc1_weight = np.array([[ 4.4037123 , -2.9683902 , -4.4077654 ,  2.3313837 ,  0.05330967], [-1.0420023 ,  3.5323772 , -1.5059234 ,  4.3279686 , -4.243471  ]], dtype=np.float32)
fc1_bias = np.array([-2.0229015, -2.446563 , -2.7381809, -2.715235 , -1.9951458], dtype=np.float32)
fc2_weight = np.array([[ 2.7341564, -2.7900338], [ 3.049221 , -3.114146 ], [ 2.761332 , -2.8246257], [ 3.0681298, -3.1184993], [ 2.8039508, -2.8363247]], dtype=np.float32)
fc2_bias = np.array([-4.372014,  4.457383], dtype=np.float32)

fc1_out = np.matmul(inp, fc1_weight) + fc1_bias  # dense layer #1
fc1_act = fc1_out.copy()
fc1_act[fc1_out < 0] = 0.0  # first layer activation  # activation #1 (relu)
fc2_out = np.matmul(fc1_act, fc2_weight) + fc2_bias  # dense layer #2
fc2_act = 1.0 / (1.0 + np.exp(-fc2_out))  # activation #2 (sigmoid)

# Quantize MLP

# # Input
inp_scale, inp_zero_point = quant_parameters(inp.min(), inp.max(), bit_width=8, asymmetric=True)
inp_q = quantize(inp, inp_scale, inp_zero_point, bit_width=8)

# # FC layer 1
fc1_weight_scale, fc1_weight_zero_point = quant_parameters(fc1_weight.min(), fc1_weight.max(), bit_width=8, asymmetric=False)
fc1_weight_q = quantize(fc1_weight, fc1_weight_scale, fc1_weight_zero_point, bit_width=8)
fc1_out_scale, fc1_out_zero_point = quant_parameters(fc1_out.min(), fc1_out.max(), bit_width=8, asymmetric=True)
fc1_bias_q = quantize(fc1_bias, inp_scale * fc1_weight_scale, 0, bit_width=32)

# # FC layer 2
fc2_weight_scale, fc2_weight_zero_point = quant_parameters(fc2_weight.min(), fc2_weight.max(), bit_width=8, asymmetric=False)
fc2_weight_q = quantize(fc2_weight, fc2_weight_scale, fc2_weight_zero_point, bit_width=8)
fc2_out_scale, fc2_out_zero_point = quant_parameters(fc2_out.min(), fc2_out.max(), bit_width=8, asymmetric=True)
fc2_bias_q = quantize(fc2_bias, fc1_out_scale * fc2_weight_scale, 0, bit_width=32)

# Run inference using quantized MLP

# # FC layer 1
fc1_y, fc1_y_scale, fc1_y_zero_points = q_matmul(inp_q, inp_scale, inp_zero_point,
                                                 fc1_weight_q, fc1_weight_scale, fc1_weight_zero_point)
fc1_out_q = requantize(fc1_y + fc1_bias_q, fc1_y_scale, fc1_y_zero_points,
                       fc1_out_scale, fc1_out_zero_point, bit_width=8)

# # ReLU activation
fc1_act_q = fc1_out_q.copy()
fc1_act_q[fc1_out_q < fc1_out_zero_point] = fc1_out_zero_point

# # FC layer 2
fc2_y, fc2_y_scale, fc2_y_zero_points = q_matmul(fc1_act_q, fc1_out_scale, fc1_out_zero_point,
                                                 fc2_weight_q, fc2_weight_scale, fc2_weight_zero_point)
fc2_out_q = requantize(fc2_y + fc2_bias_q, fc2_y_scale, fc2_y_zero_points,
                       fc2_out_scale, fc2_out_zero_point, bit_width=8)

# Dequantize output of 2. FC layer         
fc2_out_deq = dequantize(fc2_out_q, fc2_out_scale, fc2_out_zero_point)

# # Sigmoid activation on dequantized output of 2. FC layer
fc2_act_deq = 1.0 / (1.0 + np.exp(-fc2_out_deq))

with np.printoptions(precision=4, suppress=True):
    print("fc2_act:\n", np.array2string(fc2_act))
    print("fc2_act_deq:\n", np.array2string(fc2_act_deq))
    print("quantized inference error:\n", np.abs(fc2_act_deq - fc2_act))

( complete script )

Using this code on the test set mentioned above for different bit widths, we can compare the final effectiveness of the implemented quantization:

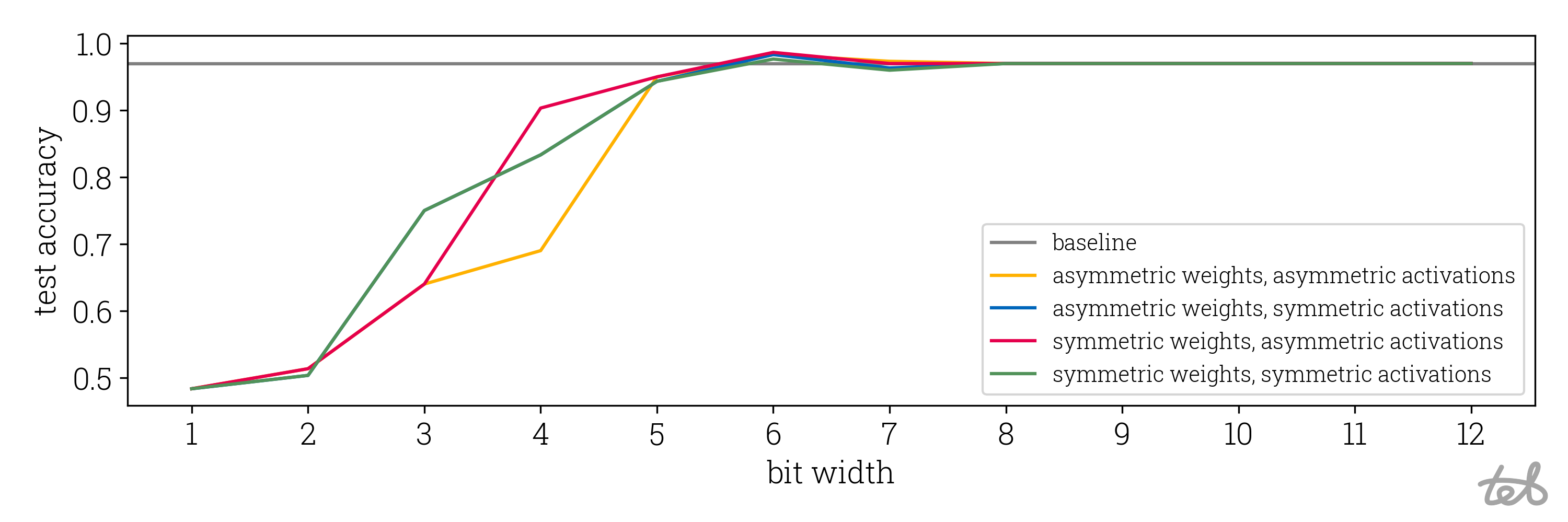Graph showing the accuracy drop for a simple MLP for different combinations of symmetrix/asymmetric quantization of weights and activations Accuracy of the quantized MLP as performed in the code above on the test split of the circles dataset. It is clear that using 8-bit quantization results in no relevant accuracy loss. We also see that accuracy drop saturates at a bit width of about 5.

Also compare the contour plots of the quantized models to the original float32 model as shown in the introduction of this post.

Part II: Expanding quantized matrix multiplication to ViT quantization

Having the five quantization functions quantize, dequantize, quant_parameters, q_matmul and requantize up our sleeves it is possible to build a small framework which is able to quantize ViT and run it without using any other packages. To achieve this we

The code snippets of this part are adapted from the repository numpy-quant which implements all necessary steps.

Getting ready: the graph structure

In order to built the computational graph, we basically create one class for Tensor's and one for Value's such that the Tensor's are connected to Value's and vice versa.

To see how this works, consider this small part of the whole computational graph of ViT (self-attention):

Visualization ViT's self attention layer
Visualization of self attention mechanism used in ViT created with netron. The five MatMul Operators are the ones we can easily quantize. You can explore the computational graph of complete ViT , ViT encoder layer and self attention interactively.

In order to differentiate between float32 and quantized Tensor's we start by creating one class for each:

class FTensor:
    def __init__(self, data: np.ndarray):
        self._data = data

class QTensor:
    def __init__(self, data: np.ndarray[Any, np.int64], bit_width: int, scale: np.float32,
                 zero_point: np.ndarray[Any, np.int64]):
        self.bit_width = bit_width
        self.scale = scale
        self.zero_point = zero_point
        self._data = data.astype(np.int64)

Tensor = Union[FTensor, QTensor]

(numpy-quant sources here and here )

We now proceed by wrapping the tensors into Value's which are connected to Node's. It's convenient to distinguish further between constant and variable tensors. The Constant Tensors correspond to trained weights of a NN while the Variable Tensors represent the Tensor's being calculated during inference.

class Constant:
    def __init__(self, name: str, outputs: List['Node'], data: Tensor = None):
        self.name = name
        self.outputs = outputs  # The nodes which use this Constant's data as input
        self.data = data

class Variable:
    def __init__(self, name: str, inputs: List['Node'], outputs: List['Node'], data: Tensor = None):
        self.name = name                
        self.inputs = inputs    # The nodes which produce this Variable's data
        self.outputs = outputs  # The nodes which use this Variable's data as input
        self.data = data        

Value = Union[Constant, Variable]

(numpy-quant source here )

The Nodes correspond to all kinds of operations, i.e. Matrix-Matrix-Multiplication, ReLU or Reshape. In order to easily import ONNX we follow the ONNX operator scheme:

class Node:
    def __init__(self, name: str, op: str, attrs: dict[str, Any], inputs: List[Value], outputs: List[Value]):
        self.name = name
        self.op = op            # The type of operation to perform, i.e. matrix multiplication
        self.attrs = attrs      # Attributes configuring the behavior of the operation
        self.inputs = inputs    # The values required to calculate the outputs of the node
        self.outputs = outputs  # The values being calculated by the node

(numpy-quant source here )

Lastly, we represent a complete computational graph by a list of Nodes's and Value's as well as the Variable's constituting the input and output of the graph:

class Model:
    def __init__(self, nodes: list[Node], values: list[Value], inputs: List[Variable], outputs: List[Variable]):
        self.nodes = nodes
        self.values = values
        self.inputs = inputs
        self.outputs = outputs

(numpy-quant source here )

We are now ready to import an ONNX model representing ONNX into this structure. Since our graph description is very similar to the one ONNX is using, the implementation is straightforward:

  1. Make the onnx model accessible in python via onnx.load
  2. Iterate over constants of the onnx model (called initializers in ONNX) and create corresponding Constant's.
  3. Iterate over the nodes of the onnx models, create corresponding Node's as well as Variable's for the onnx-node's inputs and outputs.

Details can be found in numpy-quant implementation.

Assuming we have the onnx model available at vit.onnx we can now run:

import onnx 
from numpy_quant.model import Model

# Import ONNX model to numpy-quant
onnx_model = onnx.load("vit.onnx")
model = Model.from_onnx(onnx_model)

# Print node, values, inputs and outputs of the model
print(model)

( complete script with onnx model creation )

Bringing the graph to life: Running Inference

Now that we have the ViT graph available, we can set a value for the input tensor and then iterate through the nodes to create the node's output tensors. Note that due to the import of ViT from ONNX the list model.nodes is sorted such that a Node's inputs are calculated when it is reached in the list.

model = Model.from_onnx("vit.onnx")
model.inputs[0].data = FTensor(np.random.normal((1, 3, 224, 224)))

# Iterate through nodes updating all variables in the model.
for node in model.nodes:
    inputs = [i.data for i in node.inputs]

    outputs = onnx_operator_implementation(node.op, inputs, node.attrs)

    for o, tensor in zip(node.outputs, outputs):
        o.data = tensor

( complete script )

The somewhat tedious task is to implement all necessary operations in the function onnx_operator_implementation as has been done here.

Grand Finale: Running a numpy-quantized ViT

In order to transform the ViT graph to a corresponding quantized execution graph, we create a class to represent the quantized model:

class QuantizationParams:
    def __init__(self, scale: np.float32, zero_point: Union[np.int64, None]):
        self.scale = scale
        self.zero_point = zero_point

class QModel(Model):
    def __init__(self, nodes: list[Node], values: list[Value], inputs: List[Variable], outputs: List[Variable],
                 bit_width: int, quant_params: dict[str, QuantizationParams]):
        """
        quant_params: value name -> quantization parameter
            Store the quantization parameters as obtained by numpy_quant.numpy_quantization.quant_parameters
            for every value in the model.
        """
        super(QModel, self).__init__(nodes, values, inputs, outputs)
        self.bit_width = bit_width
        self.quant_params = quant_params

(numpy-quant source here and here and)

In particular, the quantized model keeps a dictionary storing all quantization parameters. In order to obtain those parameters for the Variable's a reference input data set must be provided to the quantization routine. These parameters allow to always convert tensors to their quantized version.

In order to quantize all matrix-matrix-multiplications ("matmul") of ViT we can actually use the same computational graph for the quantized model, only changing the following aspects:

Having all of this set up we can harvest our fruits and see evaluate the performance drop of the ViT for Image Classification:

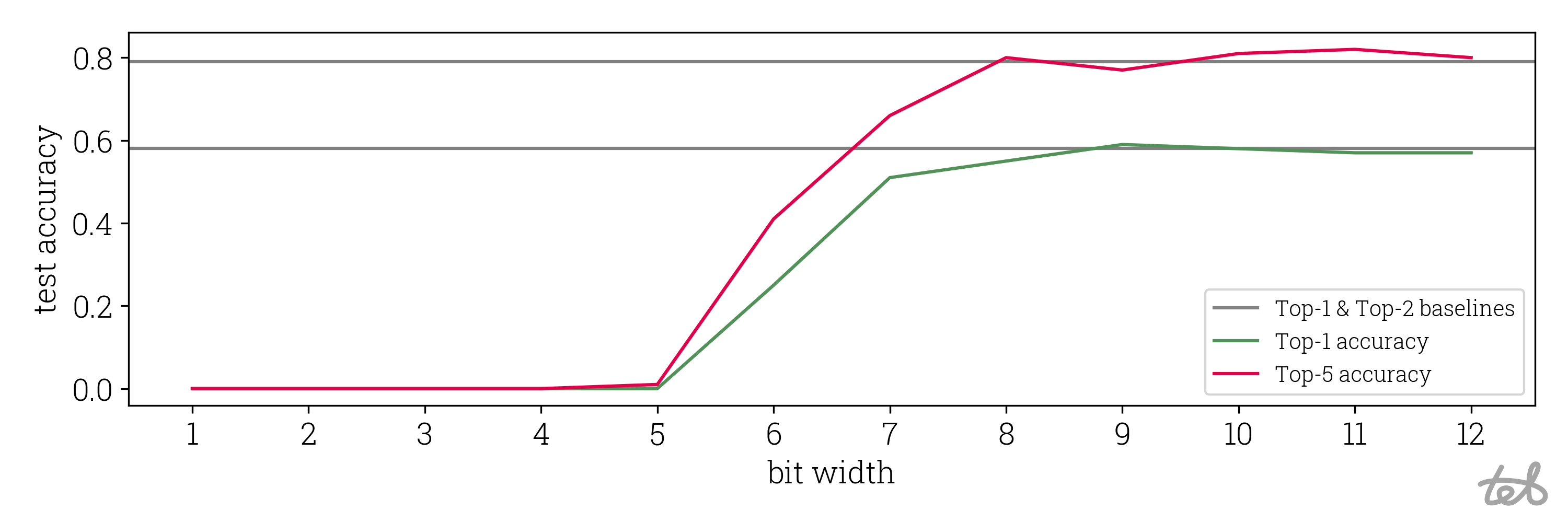Graph showing the accuracy drop for presented ViT quantization Accuracy drop of presented ViT quantization. The ViT has been adopted from google/vit-base-patch16-224. Weights are quantized symmetrically and activations asymmetrically. The accuracy has been calculated using 100 validation images taken from Maysee/tiny-imagenet.

Conclusions and where to go next

We have seen that quantizing a neural network as complicated as ViT in python & numpy comes back to

Using that, we found that the simple quantization method developed is able to quantize ViT reasonable well for a bit width of 8 but shows a severe accuracy loss starting at a bit width of 7.

To improve the quality of the acquired quantization, we could i.e. follow one of those methods:

website design inspired by motherfuckingwebsite.com